기초통계학 - 기술통계_수치적 해석
'자료 분석의 최종 결과는 그 자료의 특성을 나타내는 수치로 제시!'
Ex) 중심위치, 평균은??? 등...
중심위치
n개의 데이터... x1, x2, x3 ..... , xn
x_i : i번째 x값
n을 포본크기(Sample size)라 한다.
1) 표본 평균(sample mean)
표본들의 합을 표본의 크기로 나눈 값. ' - ' 를 통해서 평균이라 표시 'bar'라고 읽음.
편차 : 평균에서 떨어진 정도
= i번째 값 - 평균
2) 표본비율(sample propotion)
관측값이 어떤 범주에 속하여 이진분류후 범주에 포함되는 비율을 표본 비율이라 함.
표본비율 또한 일종의 표본 평균으로 이해할 수 있음.
3) 이상점(outlier)
중심점으로부터 특이하게 높거나 낮게 위치해 있는 데이터
표본평균의 경우 이상치에로부터 로버스트(둔감)하지 않다.
4) 표본 중앙값(sample median)
순서대로 나열하여 순서상 가운데에 위치한 값. 표본중앙값의 경우 이상치로부터 로버스트(둔감)하다.
홀수일 경우 하나의 값이 정해지지만 짝수일 경우 중앙에 위치한 두개의 값의 평균으로 값을 사용.
5) 표본절사평균
표본중 가장 높은 값과 가장 낮은 값을 제외한 평균. 값은 상위, 하위 %로 백분위수를 적용할 수 있음.
Ex) 피겨스케이팅, 체조 등 스포츠에서 심판들의 점수를 집계하여 최고, 최저를 제외한 평균 점수를 책정 -> 조작 방지
6) 표본최빈값(sample mode)
가장 많이 등장한 값으로 중심위치로 사용.
퍼짐의 측도
중심의 위치 만큼 중요한 통계 지표중 하나로 '산포'라고함. 자료가 얼마나 퍼져있는지 확인할 수 있을 뿐 아니라 중심위치가 얼마나 안정적인지를 나타낼 수 있는 지표.
1) 범위
가장 큰 값과 가장 작은 값을 빼서 범위를 설정. 이상점에 굉장히 민감하게 반응함.
2) 사분위수
데이터를 동일하게 4등분한 3개의 구분선(Q1,Q2,Q3)으로 표현 (0, 25, 75, 100)
사분위 범위(IQR) = Q3(75%) - Q1(25%)
3) 상자 그림(box plot)
1. 사분위수의 구분 Q1,Q2,Q3로 상자를 형성.
2. +- 1.5IQR의 연장선을 긋고 그 안에 있는 가장 큰 값, 작은 값들로 추가적 라인을 형성.
3. 이후 그 외 값들은 점으로 표현. 점을 이상치(Outlier)라고 함.

4) 분산과 표준편차
1) 거리(Distance)
거리란? 임의의 점 a,b,c에 대해서 다음과 같을때 거리라한다.
- a = b 이면 D(a,b)는 = 0 이고, 그 역도 성립한다.
- D(a,b) = D(b,a)
- D(a,b) <= D(a,c) + D(c,b)
- Ex) D(a,b) = | a - b |, D(a,b) = (a-b)^2
2) 관측값들의 거리 합

중심위치를 a(x_j)라 할때 중심위치는 어디로 정해야할까?
-> 중심위치는 모든 값들과 비교해 가장 짧은 위치에 있는 것이 최적의 값이다.
제곱식의 경우에는 미분이 가능해 a의 값은 x의 평균이되고 절대값의 경우 미분이 되지 않기 때문에 x의 중앙값이 된다.

3) 분산과 표준편차
분산은 n개의 편차를 이용하여 구하는것 같지만 실제로 편차의 합이 0이다라는 제약조건 때문에 n-1개를 사용한다.
예를 들어서 x1, x2, x3, x4가 있을때 중심지점 a로부터 x1,x2,x3의 거리가 각각 -3, -2, 5 일때 x4와 a와의 거리는 0일 수 밖에 없다. 왜냐하면 편차의 합은 항상 0이기 때문이다. 사실 x1~x3까지의 값이 어떤값에 상관없이 x4값은 앞 3개의 값에 종속되버린다. 그래서 n-1개의를 사용하고 이것을 자유도(degree of freedom)이라 한다.

표준편차는 분산을 우리가 인식하기 쉽게하기 위한 단위로 변경하는 것이다. 거리라는 개념을 사용했으니 m의 개념으로 가보면 미분이 가능한 식을 사용하기 위해 제곱이 씌워진 식을 사용헀는데 그러면 단위 역시 제곱미터가 된다. 그러면 우리가 인지해야하는 단위는 선이 아니라 면으로 바뀌게 된다. 그러면 다시 우리가 쉽게 인지할 수 있는 선의 단위로 돌리기게 되는데 이를 표준편차라 한다.

4) 표준화
간단하게 수능점수에서 일반점수, 표준점수, 백분위 이렇게 구분이 되어있는 것중에서 표준점수라고 생각하면 된다. 표준 점수는 단순히 점수가 아니라 그 해의 수능이 언어, 수리가 물수능, 불수능으로 갈리는 경우가 있는데 원점수로는 이 부분이 반영되어 있지 않다. 그렇기에 단순히 점수로만 과목 비교가 어렵다 하지만 표준화를 통해서 표준점수가 나오고 이를 통해 응시자들중 과목별 내 위치가 어느 위치에 있는지를 알 수 있게된다. 이를 위해서 평균을 0, 표준편차를 1로 만들어 점수단위에 영향을 받지 않게 조정하여 비교가 가능하도록 만든다.
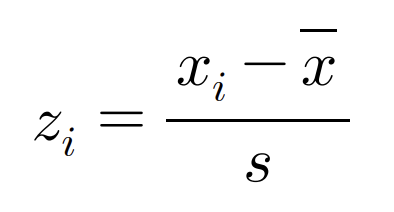


5) 변동계수
표준편차만으로 그룹을 비교하기 어려운 경우가 있는데 이때 평균으로 표준편차를 나누어 보정해주는 작업을 거치는데 이를 변동계수라한다.
Ex)선진국과 후진국의 임금의 차이. 선진국은 편차가 크지만 후진국은 작을 것이다. 단순 순치 비교는 어렵다. 이때 평균으로 표준편차를 나누어 비교를 진행한다.
공분산과 상관계수
두 수치형 변수간에 직선관계가 있는지 확인하기 위해 산점도를 통해 확인한다.
공분산은 직선관계를 확인하기 위해 사용하는데 그 정도가 어느정도인지는 파악할 수가 없다. 공분산의 값으로 음수냐 양수냐를 알 수있지만 그 관계가 얼마나 강한지를 판단하기 위해서 위에서 언급한 평균이 0, 표준편차를1로 만드는 표준화를 진행하게 된다. 그렇게되면 상관계수를 알수 있게되고 이게 상관에서 가장 널리 사용되는 피어슨의 상관계수가 된다. 이 상관계수는 -1<=r<=1범위를 갖고 1에 가까울수록 양의 직선에 몰려있는 산점도, -1에 가까울수록 음의 직선에 몰려있는 산점도가 되고 0에 가까울수록 직선형태가 아닌 형태의 산점도 임을 알 수 있다.
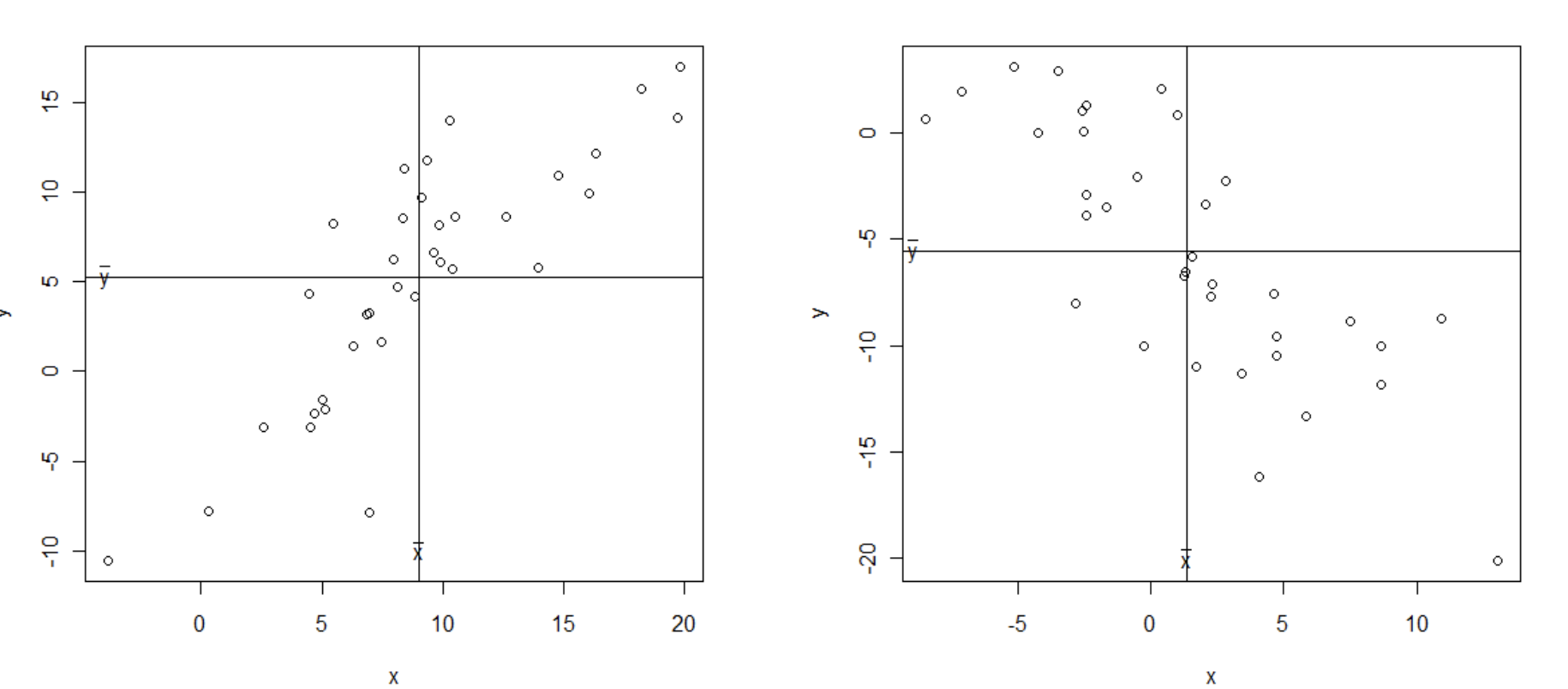

상관관계를 사용하게 되면 가장 많이 사용하게 되는것이 피어슨의 상관계수(r)인데 이는 단순히 변수간 직선관계에 대한 파악을 할 뿐 변수간의 관계가 있냐 없냐를 판단할수가 없다. 곡선형태의 관계라면 r은 0에 가까운 값이 나오게 될 것이고 이는 직선관계가 없을뿐 관계가 없다라고 할 수 없기때문에 산점도를 그려서 직접 어떤 관계인지 확인할 필요가 있다.