| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- BERTopic
- 코사인 유사도
- 클래스 분류
- 피파온라인 API
- 원신
- 데벨챌
- 포아송분포
- 블루아카이브 토픽모델링
- 구글 스토어 리뷰
- NLP
- 데이터리안
- 조축회
- LDA
- 블루 아카이브
- 토픽 모델링
- 옵티마이저
- Tableu
- Roberta
- 개체명 인식
- geocoding
- 트위치
- 붕괴 스타레일
- 문맥을 반영한 토픽모델링
- CTM
- 데이터넥스트레벨챌린지
- SBERT
- KeyBert
- Optimizer
- 자연어 모델
- 다항분포
- Today
- Total
분석하고싶은코코
다양한 유사도의 종류(1) 본문
"코사인 유사도를 선택한 이유와 다른 유사도는 무엇이 있을까?"
위 질문을 받아보니 명확한 이유를 답할 수 없었습니다. 그냥 유사도에 대해서 학습할때 코사인 유사도를 많이 사용하니 코사인 유사도를 사용하는거지라는 생각만 들었습니다. 그래서 이번 포스팅에서는 다양한 유사도의 종류에 대해서 알아보도록 하겠습니다.
다양한 유사도들에 대해서 알아볼 예정이기에 하나의 포스팅보다는 여러 포스팅으로 나눠 진행합니다.
유사도(Similarity)?
다양한 유사도들에 대해서 알아보기 이전에 유사도(Similarity)란 무엇인가에 대해서 부터 이해하고 다양한 유사도들에 대해서 살표보겠습니다.
유사도란 A와 B가 서로 얼마나 비슷한가? 가까운가? 닮아있는가? 등의 단어로 표현할 수 있습니다. 즉 두 대상을 비교하는데 얼마나 유사한지를 나타내는 척도라고 생각하면 될 것 같습니다. 이 유사도를 구하는 방법에는 밑에서 살펴볼 다양한 접근법들이 있습니다.
공통 이웃 유사도(Common Neighbor Similarity)
공통 이웃 유사도는 네트워크 서비스 분석이나 그래프 이론에서 주로 사용되는 유사도 접근법입니다. 공통 이웃 유사도는 두 대상 간의 유사성을 결정할 때 공통 이웃의 수를 고려하여 계산하게 됩니다. 즉, 두 대상이 많은 공통 이웃을 가질수록 유사성이 높은 결과를 얻게 됩니다. 공통 이웃 유사도를 구하는 수식은 다음과 같습니다.
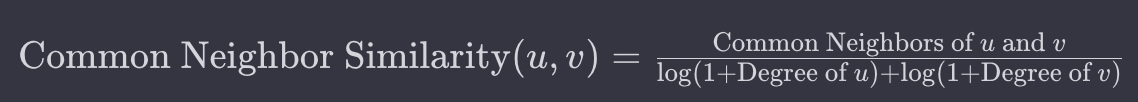
- Common Neighbors of u and v : u와 v가 공통으로 갖는 이웃을 의미합니다.
- Degree of u / Degree of v : u 혹은 v에 연결된 이웃의 수를 의미합니다.
이 공통 이웃 유사도를 활용하는 대표적인 곳은 소셜 네트워크 서비스(SNS)에서 팔로우, 팔로워, 친구 관계를 통해 계산할 수 있고 이를 통해 새로운 추천 목록을 만들어 줄 수 있습니다.
+ Admic_Adar
Admic_Adar는 공통 이웃 유사도 방법에서 좀 더 발전 시켜 만들어진 유사도 측정 방법입니다. 기본적으로 공통 이웃 유사도의 접근 방법을 사용합니다. 두 대상(노드)끼리 공통된 이웃을 기준으로 유사도를 측정하지만 Admic_Adar는 공통 이웃의 요소중 특정 이웃에 중요성(가중치)를 주어 두 노트간 유사도를 구하는게 다른점이라고 할 수 있습니다. 그래서 수식은 아래와 같이 기본적인 공통 이웃 유사도를 구하고 이후에 특정 이웃(w)에 대한 가중치를 적용하는 수식이 더해지게 됩니다.

해당 유사도는 역시 소셜 네트워크 서비스에서 사용이 대표적입니다. 예를들어 서비스하는 제품에 뮤지션이 중요한 피처임을 찾았다면 고객들에게 추천 목록을 만들어줄때 뮤지션에 대한 가중치를 주어 추천 목록을 만들어줄 필요가 있게 되겠죠. 이 경우 팔로우, 혹은 친구의 경우 뮤지션에 대한 요소에 가중치를 주어 유사도를 구하게 된다면 보다 정교한 추천 목록을 만들어 줄 수 있게 됩니다.
자카드 유사도(Jaccard Similartiy)
자카드 유사도는 대상을 하나의 집합으로 보고 비교 대상(집합) 간의 유사도를 구하는 접근법입니다. 두 집합 간의 비교를 하기에 사용하는 데이터는 두 집합의 교집합과 합집합입니다. 이를 통해 두 집합간의 유사도를 구하게 됩니다. 수식은 아래와 같습니다.

자카드 유사도를 활용할 수 있는 부분은 대표적으로 NLP(자연어처리)분야에서 문서, 문장 간의 유사도를 구할 때를 생각해볼 수 있습니다. 예를 들어 문서간 유사도를 자카드 유사도로 구한다고 했을때 핵심이 되는 단어를 선택하고 해당 단어가 얼마나 들어 있는지에 대해서 자카드 유사도를 적용해볼 수 있습니다. 이를 통해 문서간 유사도를 측정할 수 있게 됩니다.
선호적 연결성 유사도(Preferential Attachment Similarity)
선호적 연결성 유사도의 접근 방법은 새로운 노드(아이템)이 발생했을때 이미 많은 노드들이 서로 연결되어 있고 이를 기반으로 연결(추천) 노드를 선택하게 되는데 이를 해당 노드의 이웃수에 비례하여 선택한다는 접근방법입니다. 복잡할 필요 없이 정말로 각 노드의 이웃수에 기반한 유사도 구하는 방법이기에 수식도 간단합니다. Degree(u), (v)는 각각 u,v에 연결된 이웃의 수를 나타냅니다.

선호적 연결성 유사도는 네트워크 분석에서 주로 사용됩니다. 이 선호적 연결성 유사도는 앞 서 생겨난 노드(아이템, 유저 등..)이 먼저 생겨서 활동을 했고 그로 인한 연결점이 생겨있고 이를 기반으로 유사도를 구한다는 접근법이라 데이터가 전혀 없을때 노드간 유사도를 구하기는 어려운 접근법입니다.
코사인 유사도(Cosin Similarity)
코사인 유사도는 벡터간 유사도를 구하는 가장 보편화된 유사도 접근 방법입니다. 코사인 유사도가 이전보다 많은 관심(?)을 받게 된 계기는 NLP(자연어처리) 분야가 급부상이 가장 큰 요인으로 생각됩니다. 이전까지는 각 피처들을 벡터화 해서 벡터 공간에서 서로 유사도를 구하는 접근 방법이 없던 것은 아니었지만 NLP가 급속도로 성장하고 비정형 데이터를 활용한 다양한 모델들이 나오면서 자연어처리 분야에서 가장 많이 쓰이는 코사인 유사도도 같이 관심을 받게 되었습니다.
각 피처들 간의 유사도를 구하기 위한 방법으로 코사인 유사도 말고 맨하튼(Manhattan), 유클리디안(Eclidean)과 같은 거리를 구하는 방법으로 유사도를 구할 수 있었지만 그 중에서도 코사인 유사도가 주목받은 이유는 벡터 간 유사도를 구할때 맨하튼, 유클리디안은 차원이라는 요소를 고려해야하지만 코사인의 경우 벡터의 방향만을 고려한다는 점이 다른점의 핵심이라고 할 수 있습니다.

코사인 유사도는 NLP에서 뿐만 아니라 다른 분야에서도 사용될 수 있습니다. 즉 어떤 대상의 특징들을 하나의 벡터로 변환하여 각 벡터간의 유사성을 확인해 보는 방식으로 접근하는 것이죠. 그래도 대표적으로 사용하는 분야는 NLP로 텍스트간 유사성을 찾아내는 것이 대표적인 사용으로 볼 수 있습니다.
피어슨(Pearson)
피어슨은 유사도(Pearson Similarity)로 불리기도 하지만 더 범용적으로 불리는 것은 피어슨 상관계수(Pearson Correlation Coefficient) 입니다. 피어슨 유사도는 두 변수간 선형적 관계를 통계적으로 나타낼 수 있는 지표입니다. -1에서 1사이 값을 갖게 되고 -1에 가까울 수록 음의 상관, 1에 가까울 수록 양의 상관, 0에 가까울수록 상관이 없다로 해석할 수 있는 지표가 됩니다. 피어슨 유사도는 통계적 지표로 두 변수의 공분산과, 표준편차를 사용합니다. 공분산과 표준편차에 대한 설명을 하면서 자연스럽게 피어슨 상관계수에 대한 이야기가 이어지니 찾아보시길 권장드립니다.

피어슨 유사도는 언급했지만 두 변수간 '선형'관계를 나타내는 지표로 0에 가깝다면 산점도를 그려서 해당 변수들이 어떤 관계를 갖고 있는지 직접 확인해볼 필요가 있습니다. 정말로 전혀 관계가 없는 산점도가 나올 수 있지만 2차 함수 이상의 비선형 관계를 갖고 있을 수 있기 때문입니다. 따라서 산점도를 그려 두 변수간의 상관이 비선형적 관계임을 파악했다면 피어슨 상관이 아닌 스피어만(Spearman)이나 켄달(Kendall) 상관계수를 통한 접근을 해볼 수 있고 PDA와 같은 방법을 통해 차원을 축소하여 선형적 관계를 만들어 내는 접근 방법으로 피어슨을 활용해 볼 수 있습니다.
유사도에는 많은 유사도들이 있지만 상황에 맞는 유사도를 선택하는 것도 분석가로서 중요한 역량이라고 생각됩니다. 사실 이 부분은 이전에 컴퓨팅 자원이 여유롭지 못할때나 통하는 이야기가 아닐까도 생각됩니다. 요즘은 워낙 컴퓨팅 자원들이 성능이 좋아서 직접 많은 유사도들에 대해서 샘플 데이터들을 적용해보고 데이터를 통해 최고의 결과를 도출할 수 있는 유사도 방식을 선택 가능한 상황이라고 생각합니다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘 (0) | 2022.11.11 |
|---|---|
| heap / heapq 모듈 (0) | 2022.11.11 |
| 시간복잡도 (0) | 2022.11.11 |
| BFS, DFS 알고리즘 (0) | 2022.11.03 |
| 자료구조와 알고리즘 + 코딩 테스트 문제풀이 (0) | 2022.10.20 |

