| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 옵티마이저
- Optimizer
- 피파온라인 API
- KeyBert
- 원신
- 데이터넥스트레벨챌린지
- Roberta
- Tableu
- 문맥을 반영한 토픽모델링
- 개체명 인식
- SBERT
- 붕괴 스타레일
- 블루아카이브 토픽모델링
- 코사인 유사도
- geocoding
- 클래스 분류
- 포아송분포
- CTM
- 구글 스토어 리뷰
- 트위치
- 자연어 모델
- 토픽 모델링
- 다항분포
- 블루 아카이브
- NLP
- 데이터리안
- BERTopic
- 데벨챌
- LDA
- 조축회
- Today
- Total
분석하고싶은코코
기초 통계학 - 포아송, 기하, 음이항, 다항분포 본문
포아송분포
포아송분포는 흔히 알려진게 단위시간(범위) 내에 어떤 사건이 발생하는 횟수를 나타내는 이산확률분포를 이야기합니다.
그렇다면 이 포아송분포는 언제 사용할까요? 앞서배운 이항분포에서 모수(Parameter) n과 p가 존재했는데 여기서 n이 너무 크다면 이항분포를 사용하기 어렵습니다. 거기에 더해 p가 충분히 작은 경우 이럴때 이항분포의 근사확률 계산에 포아송분포를 사용하게 됩니다. 쉽게 이항분포는 횟수를 포아송은 비율을 본다는 느낌으로 이해하시면 쉽게 이해가 될 수 있습니다. 이항분포에서 n이 너무 클 경우 포아송으로 대체할 수 있다고 했습니다. 포아송에서는 기댓값을 lambda라고 하는데 이 lambda만 알면 쉽게 포아송에 대한 확률질량함수를 구할 수 있습니다. 실제로 Python scipy를 통해 포아송을 구현할때도 평균(E(x) == lambda)만 안다면 쉽게 구현이 가능합니다.


예로 들어보면 1년에 발생할 비행기 사고에 대한 분포를 구해보고자 합니다. 1년에 운행은 1만번 된다고 가정하고 비행기 사고가 날 확률은 12만분의 1이라고 합시다. n은 충분히 크고 p는 충분히 작습니다. 이때 포아송 분포와 이항분포에서 사고가 한 번 일어날때를 확인해보겠습니다.
그럼 Python에서 구현해보기 위해서 1년에 비행기가 10만번 운행이되고 그 안에서 사고가 날 확률이 12만분의 1이라는 조건에 이항분포와 포아송분포를 구현해보겠습니다. 같은 조건에 이항분포와 포아송분포의 결과값은 0.82641%까지는 동일하고 이후에 달라지는걸 볼 수 있습니다. 굉장히 작은 차이가 있게 됩니다.
from scipy.stats import poisson, binom
p = 1/1200000 # 사고 발생확률
n = 10000 # 비행기 운행수
mu = n*p # lambda
target = 1 # 사건 발생수
print("포아송 : ", poisson.pmf(target, mu))
print('이항분포 :', binom(n,p).pmf(1))포아송 : 0.008264177438657297
이항분포 : 0.008264184296782471
또한 포아송분포의 가장큰 특징은 분산 역시 lambda값을 갖는다는 것입니다. np(1-p)가 이항분포의 분산식인데 이항분포의 근사확률을 포아송분포를 통해 구한다 했으니 그 분산식을 이용해 분산을 구해보면 lambda(1-p)가 되는데 이떄 가정이 p는 충분히 작은 확률이라 했기에 결국 lambda만 남아 분산이 lambda가 나온다 할 수 있습니다. 이렇게 설명할 수 있지만 보다 정확한 설명은 밑에 식을 통하면 최종적으로 E(x)인 lambda만 남게 된다.

기하분포
기하분포는 우리가 가장 가장 흔하게 사용하는 분포중 하나입니다. 그 예로 '주사위를 눈이 6이 나올때까지 던진다.'라는 실험을 할때의 분포라고 생각하면 됩니다. 즉 베르누이 시행으로 성공과 실패가 존재하는데 이때 성공이 나올때까지 시행하는 분포입니다. 이 기하분포의 특징이라고하면 무기억성이 있습니다. 쉽게 설명하면 도박사의 오류를 생각하시면 됩니다. 도박사의 오류는 동전던지기를 할때 10번을 던졌을때 8번이 앞면 2번이 뒷면이 나왔을때 '앞면이 이정도 나왔으면 다음은 뒷면이 높을거다!'라고 생각하는 오류를 도박사의 오류라고 합니다. 근데 전혀 그렇지 않죠 11번째 던진 동전의 앞,뒤 확률은 여전이 1/2입니다.
이 기하분포는 성공할 확률이 p인 시행에서 처음으로 성공하는 시행 횟수, 실패하는 평균 시행 횟수 등을 모델링할 때 적용해 볼 수 있겠습니다. 그러면 그 예시로 앞서 이야기한 주사위의 눈이 6이 나올때까지 던진다고 했을때 4번째와 4번 이내에 눈 6이 나올 확률을 구해보겠습니다.
from scipy.stats import geom
p = 1/6 # 주사위 눈의 확률
n = 4 # 시행수
print('주사위 눈 6이 4번째 나올 확률 : ', geom.pmf(n, p))
print('주사위 눈 6이 4번 이내에 나올 확률 : ', geom.cdf(n, p))주사위 눈 6이 4번째 나올 확률 : 0.09645061728395063
주사위 눈 6이 4번 이내에 나올 확률 : 0.5177469135802469
음이항분포
음이항분포는 기하분포를 확장한 것이라 생각하면 됩니다. 기하분포는 사건에서 처음 성공할때까지 시행한 분포라면 음이항분포는 처음 성공이 아니라 n번 성공할때까지의 분포입니다. 똑같은 예시보다는 다른 예시로 참참참 게임을 예시로 들어보겠습니다. 도전자 A씨는 5명과 참참참 대결을 진행할 건데 이기면 다음상대로 넘어가고 지거나 비기면 이길때까지 반복하는 규칙입니다. 이때 A씨가 8번 이내에 모두 성공할 확률은 얼마일까요?
from scipy.stats import nbinom
p = 1/3 #확률
n = 8 # 시행수
x = 5 # 성공수
k = n-x # 실패수
print('8번 이내에 5번 승리할 확률 : ', nbinom.cdf(k, x, p))8번 이내에 5번 승리할 확률 : 0.08794391098917845
** 이 음이항분포는 포아송분포의 대체로 사용할 수 있는데 그 경우가 평균과 분산이 같다는 포아송분포의 특성이 만족하지 못할때 대체해서 사용이 가능하다.


다항분포
다항분포는 이항분포의 확장 버전이라고 생각하면 됩니다. 가장 간단한 예는 가위바위보입니다. 가위바위보의 결과는 승패로 나눌수가 없죠. 왜냐하면 동일한 수를 냈을떄 우리는 무승부라고 하게 됩니다. 그러면 우리가 알고 있던 베르누이 시행의 결과값이 2개이다라는게 깨지게 됩니다. 이렇게 결과가 2개뿐 아니라 그 이상의 결과값을 갖고 있을때 k번 시행을 하게 됐을때 이를 다항분포라고 합니다. 이를 쉽게 표로 보면 아래와 같습니다.

이 표를 가위바위보의 예로 바꾸어보겠습니다.
| 시행 | 승 | 무 | 패 |
| 1 | O(1) | X(0) | X(0) |
| 2 | X(0) | O(1) | X(0) |
| 3 | X(0) | O(1) | X(0) |
얼추 느낌이 오시나요 각 시행에서의 각 결과값에 대한 합은 당연히 하나의 확률(Probability)이기 때문에 1입니다. 따라서 하나가 결과가 발생했고 그 값을 1이라 했을때 나머지 값들은 더이상 발생하지 않기에 값은 0이 되는거죠. 또한 각 시행은 독립적이기에 다음과같이 정리할 수 있습니다.

이러한 다항분포의 문제는 무엇이 있을까요? 간단하게 카페음료인 라떼를 예로 들어 보겠습니다. 시럽이 바닐라,카라멜 2종류, 우유가 일반, 두유 2가지 이렇게 있다고 가정을 해보겠습니다. 그렇다면 나올 수 있는 음료의 종류는
바닐라라떼, 카라멜라떼, 바닐라두유라떼, 카라멜두유라떼 4가지가 나올 수 있겠죠. 이때 메뉴들의 한 달 판매비율을 확인해봤더니 10:2:3:1이라는 비율이 나왔습니다. 장사를 하는 입장에서는 당연이 수요에 대한 예측이 중요할 것입니다. 이때 카페 사장님은 내일 판매수량을 20,4,7,2잔으로 각각 예측했다고 해봅시다. 실제로 이렇게 팔릴 확률은 어떻게 될까요?
from scipy.stats import multinomial
# 예측 수량
v_l = 20
c_l = 4
v_sl = 7
c_sl = 2
menu_pred = [v_l, c_l, v_sl, c_sl]
n = sum(menu_pred)
# 판매비율 10 : 2: 3 : 1
v_lP = 10/16
c_lP = 2/16
v_slP = 3/16
c_slP = 1/16
menu_p_lst = [v_lP, c_lP, v_slP, c_slP]
print('예측 수량대로 판마 됐을 때 : ', multinomial.pmf(menu_pred, n, menu_p_lst))예측 수량대로 판마 됐을 때 : 0.00948197125291076
이런 예측도 해볼수 있지만 하나에 대해서만 관심이 있을 수 있습니다. 예를들어 바닐라 라떼에만 관심이 있다면 나머지 3개음료는 하나의 그룹으로 묶어서 이항분포 형태로 사용할 수 있습니다.
추가로 확인해볼 수 있는 것은 공분산과 상관관계가 있습니다. 이전까지는 베르누이 시행으로 결과값이 2가지로만 했지만 이제는 나올 수 있는 값들이 2개 이상으로 각 결과값끼리에 대한 상관까지도 확인을 해볼 수 있습니다. 우선 공분산은 다음과 같습니다.
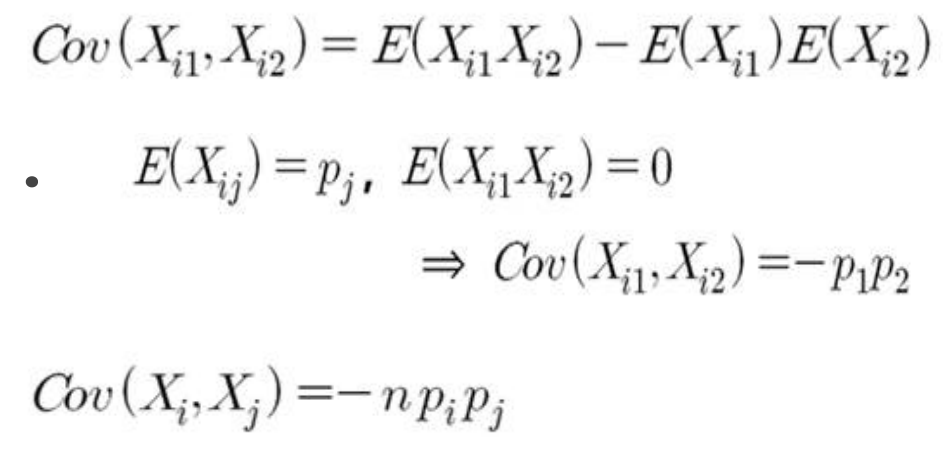
상관관계는 다음과 같은데 한가지 생각해볼 부분이 있습니다. X_i와 X_j의 상관계수는 음의 상관을 갖는데 당연히 한쪽이 결과가 많으면 다른쪽은 줄어들겠죠? 그런데 이때 두 개의 성공확률이 같이 커지면 그 상관관계가 강해진다는 점이 특징입니다. 왜냐하면 한 쪽이 높아서 많이 나오는데 다른쪽도 높다고 결과가 증식하는 것은 아니기 때문이죠.

다음은 상관관계를 확인할 수 있는데 여기서 중요한 개념인 오즈(odd)라 불리는 식이 등장합니다. 이 식은 간단하게 성공확률/실패확률입니다. 오즈가 중요한 개념이라 우리가 흔하게 일상에서 사용했던 예제를 들어보고 넘어가겠습니다. 4년마다 열리는 월드컵은 많은 국민이 관심갖는 관심사입니다. 그런데 이 월드컵에는 당연히 나라마다 상대전적이 존재할 것입니다. 이때 항상 계산하는게 있죠 상대전적을 통해서 이길 확률이 N배 높다/낮다!!라고 이야기를 많이하죠.
'통계' 카테고리의 다른 글
| 통계학 - 추정과 검정(1)_추정법 (0) | 2023.09.25 |
|---|---|
| 기초통계학 - 정규분포(Normal Distribution) (1) | 2023.09.24 |
| 기초 통계학 - 베르누이 실행, 이항 분포와 초기하 분포 (0) | 2023.09.21 |
| 기초 통계학 - 확률변수와 기댓값 (0) | 2023.09.20 |
| 기초 통계학 - 확률(2) (0) | 2023.09.19 |




