| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 트위치
- CTM
- BERTopic
- 자연어 모델
- Roberta
- geocoding
- 개체명 인식
- 조축회
- 블루 아카이브
- LDA
- 데벨챌
- 다항분포
- 코사인 유사도
- 포아송분포
- 데이터넥스트레벨챌린지
- 붕괴 스타레일
- 클래스 분류
- 원신
- 피파온라인 API
- 토픽 모델링
- KeyBert
- NLP
- 구글 스토어 리뷰
- Tableu
- 블루아카이브 토픽모델링
- 데이터리안
- Optimizer
- 문맥을 반영한 토픽모델링
- 옵티마이저
- SBERT
- Today
- Total
분석하고싶은코코
통계학 - 추정과 검정(1)_추정법 본문
지금까지 앞서 작성한 기초통계학의 내용은 추정과 검정을 하려는 기반을 쌓은 것이라고 볼 수 있다. 추정은 데이터로부터 확률분포를 찾아내는 역설계 과정이다. 추정을 통해 데이터는 확률변수로 바뀌게 되고 검정은 이러한 추정이 어느 정도의 신뢰성을 가졌는지 알아보는 과정이다. 검정을 통해 추정 결과가 믿을만한지 아니면 믿을만한 추정을 위해 데이터가 더 필요한지를 알 수 있다.
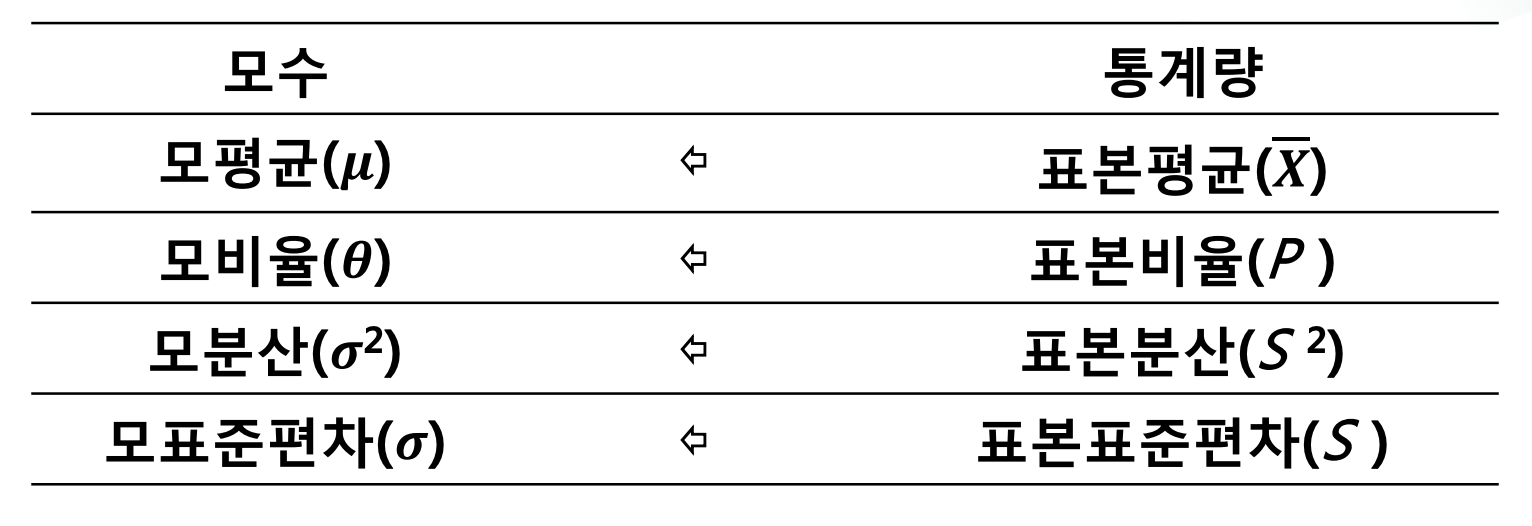
앞서 서술했던 기초통계학의 모든 내용들은 '모집단 -> 표본'의 과정에 집중했다면 통계학은 그 역인 '표본 -> 모집단'을 추론 및 검정하는 과정을 하게 된다. 그 과정은 표본들이 어떤 확률분포를 따르는지 찾아내고 확률분포의 모수가 무엇인지 찾아내는 것이다. 그렇게 찾아냈다면 이제 추정하고자 하는 모집단의 모수를 추정하는 작업을 하게 된다. 여기서 모수를 추정하는 방법은 대표적으로 3가지가 있다.
- 적률법(method of moment)
- 최대가능도
- 베이지안 추론
저는 이론적으로 가장 확률이 높은 모수를 추정하는 최대가능도와 모수를 하나의 상수가 아닌 확률변수로 보고 추정하는 벵지안 추론 두 가지를 다뤄보겠습니다.
최대가능도 추정법(점 추정)
적률법에 대한 자세한 설명은 하지 않았지만 적률법은 해당 모멘트(순간)에서의 모수 값을 구하는 것인데 이는 그 모수가 확률이 가장 높은 모수이라고 단정할 수 없습니다. 이런 부분을 보완할 수 있는게 최대가능도 추정법입니다.
앞서 기초통계학에서 배울때는 항상 대부분의 예시 문제에서 확률에 대한 정보가 포함되어있는 문제들만 봤었습니다. 그런데 현실적인 문제에서는 대부분 확률을 알지 못하죠. 상황 자체가 발생했고 그 결과값은 있지만 그 확률은 알지 못하는게 일반적입니다. 확률이 모수가 됩니다. 이 과정에서 가능도(Likilhood, 우도)라는 개념이 나옵니다. 이전에 우리가 확률을 알고 있을때는 확률변수에 대한 분포로 확률질량(밀도)함수를 통해 확인했지만 이제는 알 수가 없습니다. 모집단의 모수가 블라인드 된 상황에서 분포를 만들어 낼 수 없기 때문이죠. 하지만 이제는 확률변수가 정해졌고 결과를 알고 있는 반대 상황이기 떄문에 다른 분포를 만들어 낼 수 있습니다. 그게 𝐿(𝜃;𝑥)로 표현하고 가능도함수라고 합니다. 즉, 최대가능도 추정법(Maximum Likelihood Estimation, MLE)은 주어진 표본에 대해 가능도를 가장 크게 하는 모수 𝜃를 찾는 방법이다.
Python을 통한 코드를 실행하기 전에 간단한 예를 통해서 이해해보고 이를 구현해보겠습니다.
𝑿 ~ 𝑩(10, 𝜽)라는 X가 있습니다. 이때 x가 8이라는 값이 관측되었다고 합니다. 이때 𝜽라는 확률을 모를때 8이라는 관측값이 관측될 확률은 얼마일까요?

그림을 보면 0.8 근처에서 가장 높은 값이라 볼 수 있습니다. 이를 자세히 확인해보기 위해 가능도 함수를 그려보았습니다. 확률은 0에서 1사이에 존재하기 때문에 1000개의 지점을 만들고 각 확률일때의 가능도를 그려보았습니다. 위에서 간단하게 확인한대로 0.8근처에서 가장 높은 가능도를 갖고 있음을 확인할 수 있었습니다.
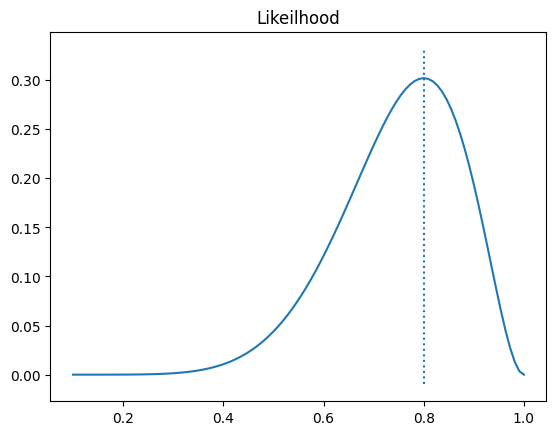
최대가능도 지점 : 0.7997997997997998
코드
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
n = 10
target= 8
p_lst = np.linspace(0, 1, 1000)
th_lst = [binom(n, p).pmf(target) for p in p_lst]
max_th = max(th_lst)
max_p = p_lst[th_lst.index(max_th)]
plt.plot(p_lst, th_lst)
plt.vlines(max_p, -0.01, max_th*1.1, linestyle=":")
plt.title('Likeilhood')
plt.show()
print('최대가능도 지점 : ', max_p)
이 최대가능도의 추정치를 구하는것은 숫자가 커지거나 복수 표본 데이터인 경우 결합확률밀도함수가 동일한 함수의 곱으로 나타나는 경우가 많아 복잡한 계산을 해야하는 상황이 발생합니다. 그런데 이때 자연로그를 통해 쉽게 연산 작업을 진행할 수 있게 됩니다. 이게 사용이 가능한 이유는 로그 변환에 의해서는 최대값의 위치가 바뀌지 않기 때문입니다. 기존에 가능도 함수는 L(𝜽)로 표기하였는데 로그가능도함수는 l(𝜽)로 표현합니다.

이러한 최대가능도 추정법을 통해서 상수형태로 추정하는것을 점추정이라고합니다. 그렇다면 이 점추정이 어떻게 좋은 점추정인가에 대한 평가는 일치성, 비편향성, 효율성 3가지 측면에서 평가가 가능합니다.
좋은 평가의 기준에 대해서 간단하게 이야기해보면 일치성은 대수의법칙을 통해 표본의 크기가 커지면 값이 수렴한다는 것에 해당됩니다. 비편향성의 경우 중심으로 분포가 표본분포를 갖는것을 이야기합니다. 효율성은 비편향 추정량이 존재할때 분포가 모수에 얼마나 더 밀집되어 있는지 확인하는 지표입니다. 대표적으로 MSE(mean square error)를 사용합니다. 값이 작을수록 더 좋은 지표라 할 수 있습니다.
베이지안 추정법(구간 추정)
베이지안 추정법(Bayesian estimation)은 모숫값이 가질 수 있는 모든 가능성의 분포를 계산하는 작업이다.
어떤 확률분포함수의 모수를 𝜇라고 할때 최대가능도 추정법에서는 𝜇를 상수로 보지만 베이지안 추정법에서는 𝜇를 확률변수로 본다. 따라서 확률밀도함수를 가지기 때문에 어떤 값들이 가능성이 높고 낮은지를 살펴보겠다는 의미로 볼 수 있다.
앞서 최대가능도를 기준으로 두 상품을 비교하는 예시를 들어보겠습니다.
- 상품 A: 전체 평가 : 10개, 긍정 평가 6개, 부정 평가4개
- 상품 B: 전체 평가 : 1,000개, 긍정 평가 670개, 부정 평가 330개
다음과 같은 상황이라고 가정해봅시다. 베르누이분포 확률변수로 모형화가 가능합니다. 최대가능도 추정법을 통해서 긍정 평가가 달릴 확률에 대해서 구해보면 A-> 0.60, B-> 0.67으로 추정할 수 있습니다. 그런데 리뷰가 남겨진 수를 보면 상대적으로 A상품의 리뷰가 10개로 너무 적습니다. 이때 A상품보다 B상품이 좋은 상품이다라 할 수 있을까요? 베이지안 추정은 이처럼 상수값으로 추정하여 잘못된 추정을 하지 않도록 도와주는 기능을 합니다.

이러한 추정법을 통해 계산된 모수의 분포는 모수와 비모수적 방법으로 표현이 가능합니다.
(1) 모수적(parametric) 방법
- 다른 확률분포를 사용하여 추정된 모수의 분포를 나타낸다. 모수 분포를 표현하는 확률분포함수의 모수를 하이퍼모수(hyper-parameter)라고합니다.
(2) 비모수적(non-parametric) 방법
- 모수의 분포와 동일한 분포를 가지는 실제 표본 집합을 생성하여 히스토그램이나 최빈값 등으로 분포를 표현합니다. 대표적으로 몬테카를로(Monte Carlo) 방법이 비모수적 방법이다.
모수적방법을 통해서 앞서 A제품에 대한 베이지안 추정법을 적용해보겠습니다. 예시는 베르누이 시행을 거쳤기 때문에 확률분포는 베타분포로 표현이 가능하고 하이퍼파라미터인 a,b는 1로 가정하고 작성해보겠습니다.

1차 추정: 모드 = 0.52
2차 추정: 모드 = 0.62
3차 추정: 모드 = 0.58import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
mu0 = 0.6 # 확률
a, b = 1, 1 # 하이퍼파라미터
xx = np.linspace(0, 1, 1000)
plt.plot(xx, sp.stats.beta(a, b).pdf(xx), ls=":", label="base") # 사전분포
np.random.seed(0)
for i in range(3):
x = sp.stats.bernoulli(mu0).rvs(50)
N0, N1 = np.bincount(x, minlength=2)
a, b = a + N1, b + N0
plt.plot(xx, sp.stats.beta(a, b).pdf(xx), ls="-.", label="b_e_{}".format(i+1)) # 사후분포
print("{}차 추정: 모드 = {:4.2f}".format(i, (a - 1)/(a + b - 2)))
plt.vlines(x=0.6, ymin=0, ymax=12)
plt.ylim(0, 12)
plt.legend()
plt.title("Bayesian estimation")
plt.show()
+ 점 추정을 통한 구간 추정과 신뢰구간
1) 구간추정
정규분포를 예로 모평균에 대한 95%신뢰구간 추정을 한다고 해보겠습니다. 모집단은 평균을 모르고 분산을 알고 있는 상황이라고 해봅시다. 그렇다면 우리가 추정해야할 모수는 평균이죠. 이 정규분포를 표준정규분포로 바꿀 수 있고 95%인 구간을 찾는다면 -0.025, 0.025의 값인 1.96을 통해 표현할 수있습니다. 아래와 같이 표현이 가능하고 각각이 L, U에 해당됩니다.

이렇게 신뢰구간을 구하고 잘못생각하기 쉬운 것이 있습니다. 예를들어 신뢰구간을(158, 162)라는 값을 구했다고 해봅시다. 그렇다면 158과 162사이에 모평균이 있을 확률이 95%인가?라는 질문에 대해서는 빈도론자 관점에서 맞다고 할 수 없습니다. 위에서 사용한 베이지안 추정법에서는 가능하지만 최대가능도 추정법에서는 틀린 대답이라는 이야기가 됩니다. 그 이유는 추정하는 값이 상수값이냐 확률변수이냐의 차이에 있습니다. 빈도론자 관점에서 추론을 상수로 했기 때문에 P(158 < 160 < 162)에 대해서 값이 0.95가 나올 수 없는 것입니다. 만약 이를 입맛에 맞춘다면 모평균에 대한 95%신뢰구간을 추정하였고 이를 많은 수를 반복했을때 그 모평균의 비율 중 95%가 해당 신뢰구간에 존재한다라고는 말할 수 있습니다. 말이 좀 어렵긴하지만 천천히 생각해보시면 이해가 될 겁니다.
2) 신뢰구간과 신뢰수준
모수를 추정할때 특정한 상수로 추정하는 점 추정이 있지만 구간을 추정할 수 있다. 구간 추정에는 신뢰구간(confidence interval)과 신뢰수준(confidence level)이 있다.
2-1) 신뢰구간
신뢰구간은 모수가 실제로 포함될것으로 예측되는 범위를 이야기합니다. ∅ 라는 모수를 구간추정하고 100(1-𝛼)% 신뢰구간이라하고 다음과 같이 표현할 수 있습니다. 범위이기에 최소값과 최대값이 존재할텐데 이때 중요하게 사용되는게 점 추정입니다.

2-2) 신뢰수준
신뢰수준은 모수를 랜덤하게 추출하였을때 그 모수가 신뢰구간에 있는 비율을 뜻합니다. 즉, 신뢰수준은 신뢰구간에 모수가 포함되어있는 것을 얼마나 신뢰할 수 있는지 확인하는 지표라고 생각하시면 됩니다.
'통계' 카테고리의 다른 글
| 통계학 - 모평균의 통계적 추론 (0) | 2023.09.27 |
|---|---|
| 통계학 - 추정과 검정(2)_가설과 검정 (0) | 2023.09.26 |
| 기초통계학 - 정규분포(Normal Distribution) (1) | 2023.09.24 |
| 기초 통계학 - 포아송, 기하, 음이항, 다항분포 (1) | 2023.09.22 |
| 기초 통계학 - 베르누이 실행, 이항 분포와 초기하 분포 (0) | 2023.09.21 |




