| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- 구글 스토어 리뷰
- KeyBert
- 트위치
- 붕괴 스타레일
- geocoding
- 블루아카이브 토픽모델링
- 다항분포
- 코사인 유사도
- 자연어 모델
- 조축회
- LDA
- SBERT
- 데벨챌
- 문맥을 반영한 토픽모델링
- Optimizer
- 데이터넥스트레벨챌린지
- Roberta
- 토픽 모델링
- NLP
- 클래스 분류
- 데이터리안
- Tableu
- 원신
- 블루 아카이브
- 개체명 인식
- 포아송분포
- 옵티마이저
- CTM
- BERTopic
- 피파온라인 API
- Today
- Total
분석하고싶은코코
통계학 - 모평균의 통계적 추론 본문
중심축량
중심축량 주축량이라고도 하는데 이 중심축량을 통해서 모평균, 모분산, 모비율에 대한 통계적 추론을 진행하게 됩니다. 중심축량은 표본을 추출하고 이를통해서 모집단의 모수 𝝁에 대한 점추정을 표본평균을 통해하게 됩니다. 또한 표본평균은 𝑵(𝝁, 𝝈^𝟐/𝒏)을 따릅니다. 이를 표준화하면 Z = (X_bar - 𝝁) / (𝝈/root(𝒏))의 형태가 됩니다. 이렇게 만들어진 Z는 모수와 통계량으로 이루어져 있고 분포는 미지모수를 포함하고 있지 않습니다. 이를 중심축량(주축량)이라고 합니다. 이 중심축량이 중요한 이유는 신뢰구간과 p-value모두 이 중심축량의 분포에서 나타내는 면적으로 연결되기 때문입니다.

모평균에 대한 통계적 추론
모평균에 대한 통계적 추론을 하기에 앞서 모집단에 대한 정의가 필요합니다. 경우는 3가지가 있습니다.
- 모집단이 정규분포 형태인 경우
- 모집단이 정규분포 형태가 아닌 경우
- 정규분포는 아니지만 표본이 충분히 크다(대표본)
- 표본이작고 이상치도 존재
- Bootstrap
1) 모집단이 정규분포 형태인 경우
모집단이 정규분포 형태일때 모평균에 대한 추론을 하기전에 알아야할 것이 있습니다. 보통 모평균을 추론한다고 할때 다른 값들이 모두 주어진다고 할 수 없습니다. 특히 평균을 모르는데 분산을 아는 경우는 드뭅니다. 그래서 여기서 새롭게 등장하는 분포가 있는데 바로 t-분포입니다.
t-분포
t 분포는 모집단 표준편차를 알 수 없을 때 표본 평균과 모집단 평균 사이 표준화된 거리를 설명하는 분포입니다. t분포는 정규분포와 매우 유사한데 다른점은 분산에 대한 값이 정규분포는 모집단의 분산을 사용한다는 것이고 t분포는 표본분포를 사용한다는데 있습니다. 그런데 이 t분포는 언제 유용하냐면 표본의 크기가 작을때 유용합니다. 그 이유는 표본의 크기가 크면 자연스럽게 분포가 정규분포에 근사한다는 것을 중심극한정리를 통해 배웠었습니다. 따라서 t-분포는 표본의 크기가 작을때 효과적이라 할 수 있습니다. 아래 그림을 통해 확인이 가능하고 그림에서 보듯 t의 크기가 커질수록 정규분포의 형태와 유사해지는 모습을 볼 수 있습니다. 이 크기를 자유도라고합니다.

그러면 이제 모평균에 대한 구간추정을 해보겠습니다. 모집단의 분산을 알 수 없기에 t분포를 활용해 구간 추정을 할 것입니다. 이제 그래서 t-분포에 대한 표현을 'v의 자유도를 갖는 (1-a) 분위수의 t-분포'를 아래와 같이 표현합니다.

이렇게 t분포를 통해 추정하고자하는 모평균의 구간P(L < T < U)은 아래와 같습니다.
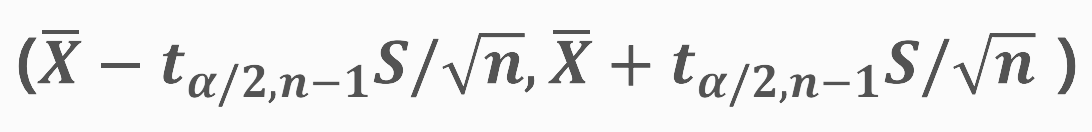
수식적인 설명보다는 직접 예제를 통해서 이해하는게 훨씬 쉽게 이해가 될 것 같습니다. 텍스트로 되어있는 숫자 자료를 가져와서 95% 신뢰구간을 구하는 과정입니다.
datas = '''
55.6 83.3 43.4 58.1 31.6 55.6 60.7 64.6 73.3 55.6 64.3 52.8 22.7 46.3
71.4 53.8 64.5 67.9 71.4 80.0 59.5 40.5 77.1 58.6 65.4 52.4 66.7 91.3
41.3 72.1 61.9 78.4 63.6 41.0 65.2 81.3 54.8 19.6 50.0 53.1 41.2 56.5
'''
nums = datas.split()
nums = list(map(float,nums))
import numpy as np
import scipy.stats as stats
df = len(nums)-1 # 자유도
mu = np.mean(nums) # 표본 평균
se = stats.sem(nums) # 표준 오차
# 95% 신뢰구간
print(stats.t.interval(0.95, df, mu, se))(53.9281267459402, 63.61473039691693)
코드를 확인해보시면 t의 신뢰구간(interval)에서 매개변수를 보면 (확인하고 싶은 신뢰구간, 자유도, 표본평균, 표본오차)를 사용하였습니다. 표준편차가 아닌 표준오차를 사용한 이유는 지난번 표집분포에 대해서 설명을 할때 '표본의 표준편차 = 표준오차'라 한다고 했기 때문에 바로 표준오차를 사용한 것입니다. 왜냐하면 표본의 표준편차는 모집단의 표준편차처럼 그냥 오메가가 아니라 오메가를 표본수의 제곱근으로 나눠준 값이기 때문에 바로 구할 수 있는 표준오차를 사용해서 변수로 사용했습니다.
stats.sem(nums), np.std(nums)/np.sqrt(len(nums))
-> 결과
(2.3982191556721455, 2.3694969320609642)
2) 정규 형태는 아니지만 표본이 큰 경우
이 경우는 너무나도 간단하게 중심극한 정리에 의해 정규분포에 근사한다는 사실을 통해서 가볍게 해결이 가능합니다. 이 경우도 Python으로 구현해보겠습니다.
이번에는 문제를 정의하고 구간추정을 해보겠습니다.
A가게에서 파는 탕후루에 대한 당 함유량에 대해서 알아보고 싶습니다. 그런데 우리는 모집단이 어떤지 모르는 상황입니다. 이때 100개의 탕후루 임의 추출하여 조사한 결과 평균함유량이 50.3mg, 표준편차는 5.11mg입니다.
이번 구간 추정에서는 Z, t분포 두 가지를 동시에 진행해보겠습니다.
import scipy.stats
import numpy as np
n =100 # 표본수
e = 0.53 # 평균
sd = 0.53 # 표준편차
print('정규분포 : ', stats.norm.interval(0.95, e, sd/np.sqrt(n)))
print('t-분포 : ', stats.t.interval(0.95, n-1, e, sd/np.sqrt(100)))정규분포 : (49.29845840390003, 51.301541596099966)
t-분포 : (49.28606513777906, 51.31393486222093)
이때 실제로 A가게의 탕후루를 먹어본 사람들은 생각보다 달지 않아 45mg정도라고 주장을 합니다. 이에 대한 검정을 진행해보겠습니다.
H0 : 𝝁 >= 45 / H1 : 𝝁 < 45
이를 우리는 5% 유의수준(p-value)에서 검정을 진행해보겠습니다.
z = 50.3 - 45 / 5.11*root(100) = 10.37181996086105이라는 값이 나왔습니다. 유의 수준 0.05는 이전에 1.645라는 값으로 이미 알고 있었습니다. 임계점인 45의 p-vaue가 10.37로 유의수준보다 높으므로 탕후루의 당 함유량이 45mg보다 적다는 리뷰(?)는 잘못된 주장이라고 할 수 있습니다.
3) 정규 형태도 아니고 표본도 작고 이상치까지 있다면...
이때는 비모수검정을 진행합니다. 비모수 검정은 모수에 대한 가정을 전제로 하지 않습니다. 따라서 모집단의 형태와 관계없이 주어진 데이터에 대해서만 진행하는겁니다. 직접 확률을 계산하여 검정하는 방법입니다. 따라서 평균이 아닌 그냥 데이터의 중심위치에 대해서 관심이 있는 것 뿐입니다. 대표적인 예시로는 부호검정이 있는데 주어진 숫자 표본 데이터에서 평균을 기준으로 분포 되어 있는 데이터들을 카운팅하고 표본에서 평균보다 높게 나올 것에 대한 p-value값을 구하는 것이 대표적인 비모수검정입니다. 비모수검정 방법은 표본의 특성에 따라 다릅니다. 다음이 대표적인 검정 방법들입니다.
- 독립적 : Mann-Whitney U Test
- 비독립적 : Wilcoxon Singed-Ranked Test
- 3개 이상의 집단 : Kruskal-Wallis H Test
- 3개 이상의 집단, 비독립 : Friedman Test
4) Bootstrap
이 경우는 우리가 사용할 수 있는 데이터는 표본뿐입니다.(이 표본의 크기를 M이라고 하겠습니다.) 그래서 우리는 표본을 통해서 추정을 진행할 것인데 대전제가 하나 있습니다. 바로 우리가 지금 갖고 있는 표본이 모집단을 대표할 수 있는 특성을 갖고 있다는 전제가 필요합니다. 이 경우 내가 갖고 있는 표본을 하나의 모집단으로 보고 새롭게 크기가 M인 표본집단을 뽑아낼 것입니다. 이때 비복원이면 모집단과 동일한 표본이 나오므로 복원추출로 표본집단을 만들어냅니다. 이를 통한 방법이 재표집(resampling)이라 합니다. 이 부트스트랩은 이후 다양한 모델에서 사용하는 기법입니다.
+ 모평균 추론을 위한 표본의 크기 설정
무언가를 추정할때는 표본의 수가 많을 수록 신뢰도가 올라갑니다. 반대로 표본수가 적으면 신뢰도가 떨어지죠. 예를들어서 여론조사를 하는데 전국민에 대해서 진행하는게 어려워서 100명을 대상으로만 했다고 한다면 신뢰할 수 있을까요? 그런데 각 이를 각 시도별 1,000명을 대상으로 진행했다고 해봅시다. 그러면 앞선 100명보다 신뢰할 수 있겠죠?? 그래서 추정을 통해 아무리 신뢰구간에 있다고 하더라도 표본의 수가 너무 적으면 신뢰도가 떨어집니다. 신뢰도를 높이고자 전국민에게 조사를 진행하면 시간과 비용이 어마어마 하겠죠. 그래서 신뢰구간을 구할때 적당한 표본의 크기를 알 필요가 있습니다.
우선 표본의 크기를 구하고자 한다면 '허용오차'를 알아야합니다. 허용 오차는 일정 크기 이상은 인정하지 않는 것으로 경계선을 말합니다. 이러한 표본의 크기를 구하는 방법은 두 가지로 나뉘는데 구간추정에 의한 크기를 구하는 방법과 가설검정에 기반한 크기를 구하는 법입니다.
우선 구간추정에 의한 크기 설정 방법인데 식은 아래와 같고 예시로 이해해보겠습니다.
'과거자료에 따르면 표준편차가(𝝈) 5라고 할 때, 95% 신뢰수준에서 오차범위가 ±1.5'라고 합니다. 이때 표본크기는 몇일까요?
이떄 우리는 신뢰수준이 95%이기에 5% 유의수준이라는 것을 알고 0.025에 해당하는 1.96이 z_a/2값이라는 것을 알 수 있습니다. 그리고 표준편차는 5라는 것도 알고 있고 오차범위(σ) 1.5라는 것까지 알고 있습니다. 이를 그대로 대입하면 (1.96 * 5 / 1.5)^2 = 42.64라는 값을 얻을 수 있고 이를통해 적어도 43개의 표본이 있어야 됨을 알 수 있습니다.

다음은 가설검정의 크기 설정하는 방법입니다. 가설검정의 표본크기를 정하는 것은 예시로는 신약개발을 하고 이에 대한 임상실험을 몇명에게 해야하는가?에 대한 물음과 동일합니다. 그래서 문제는 다음과 같습니다.
'신약 대한 예비연구에서 복용 전과 후의 차이는 평균 6이고 표준편차 15이었다고 합니다. 5% 유의수준과 80% 검정력으로 유효성 평가를 하려면 몇 명의 피험자를 대상으로 임상시험을 진행해야 하는가?'라는 질문이 나왔습니다. 이를 아래 식에 그대로 대입하면 됩니다.
- 신약의 편차(오메가) = 15
- z_a/2, 유의수준 5%의 절반인 0.025 => 1.96
- 검정령 80% -> 0.842 ( 이 부분은 표준정규분포표를 통해서 직접 확인하거나 프로그램을 통해서 확인이 가능합니다.)
- 신약과 기존약의 차이(σ(델타)) = 6
그대로 대입해보면 15^2 * (1.96 + 0.842)^2 / 6^2으로 표현이 가능합니다. 이를 계산하면 49.07로 적어도 50번의 임상실험을 진행해야 한다 이야기할 수 있습니다.
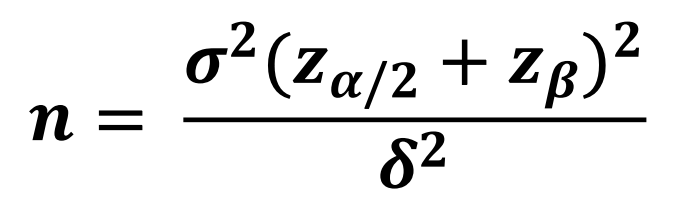
'통계' 카테고리의 다른 글
| 통계학 - 두 모집단의 평균 비교 (1) | 2023.10.04 |
|---|---|
| 통계학 - 추정과 검정(2)_가설과 검정 (0) | 2023.09.26 |
| 통계학 - 추정과 검정(1)_추정법 (0) | 2023.09.25 |
| 기초통계학 - 정규분포(Normal Distribution) (1) | 2023.09.24 |
| 기초 통계학 - 포아송, 기하, 음이항, 다항분포 (1) | 2023.09.22 |




