| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 자연어 모델
- 조축회
- SBERT
- 데벨챌
- 다항분포
- 붕괴 스타레일
- 포아송분포
- BERTopic
- 구글 스토어 리뷰
- 블루 아카이브
- 블루아카이브 토픽모델링
- 원신
- Roberta
- LDA
- 문맥을 반영한 토픽모델링
- KeyBert
- 토픽 모델링
- 클래스 분류
- 코사인 유사도
- 개체명 인식
- 데이터리안
- CTM
- 피파온라인 API
- geocoding
- Optimizer
- NLP
- 옵티마이저
- 데이터넥스트레벨챌린지
- 트위치
- Tableu
- Today
- Total
분석하고싶은코코
통계학 - 두 모집단의 평균 비교 본문
두 모집단의 평균을 비교하는데 표본들의 관계에 따라 다르게 비교가 가능합니다.
① 약을 복용한 그룹과 위약을 복용한 그룹을 대상으로 약의 효과 비교
② 혈압약 복용 전과 후의 혈압 감소 효과 비교
③ 다른 두 지역을 대상으로 대통령의 지지율을 비교
④ 수면배게의 수면 시간 효과 비교
1번과 3번의 경우 두 가지 그룹은 독립적 관계입니다. 반면 2,4번은 대응표본에 해당됩니다. 그 이유는 하나의 집단에서 두 가지 사건에 대한 비교로 독립이라고 볼 수 없는 것입니다. 대응표본의 평균 비교는 독립표본의 평균비교와 크게 다르지 않은데 핵심적으로 다른점들이 조금씩 존재하는데 이를 하나씩 알아가보겠습니다.
1) 두 모집단 비교에서의 가정
이번 글에서는 분산이 같은 경우와 다른 경우에 대해서 알아보겠습니다. 하나 더 조건이 있는데 정규성을 만족하여 정규분포를 따른다는 가정이 있습니다. 이 정규성은 고정을하고 분산만 다른 경우에 대해서 다뤄보겠습니다.
1-1) 분산이 같은 두 집단의 평균 비교
우선 2개의 그룹을 X, Y라고 했을때 각각의 표본을 다음과 같이 정의할 수 있습니다.

여기서 우리가 구하고자 하는 것은 두 그룹간의 평균에 대해 관심이 있기에 다음과 같이 표현할 수 있습니다. 이를 통해 정규분포를 따르는 두 표본평균의 선형결합을 할 수 있고 각 표본이 독립이기에 오른쪽과 같은 식으로 정리할 수 있게 됩니다.
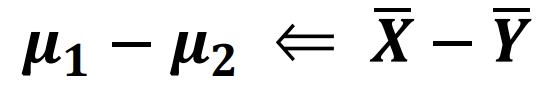

중심축량을 구하기 위한 표준화를 진행하게 되는데 여기서 문제는 오메가에 대한 값을 추정을 해야하는데 이 값이 나온 곳이 각각의 독립표본에서 나온 값으로 했기 때문에 X의 표본분산과 Y의 표본분산이 존재합니다. 둘 중 어떤걸 사용해야할지 의문이 드는데 여기서 중요한 개념인 합동표본분산이라는게 등장합니다. 이는 두 집단이 독립이고 분산이 같다는 가정을 만족해야만 아래와 같은 식이 성립할 수 있음에 주의해야합니다.


이를 통해 중심축량을 구할 수 있는데 이를 통해서 구한 중심축량의 분포는 각각 표본의 자유도를 더한 m+n-2의 자유도를 갖는 t분포를 따릅니다. 이를 통해서 (L < T < U)의 식을 정리하여 점추정 구간을 구하게 되면 오른쪽과 같은 식으로 구할 수 있게 됩니다. 이 값을 자세히 보면 아래의 값으로 정리 할 수 있습니다.
[점추정량 +- (t-분포에서 임계값) * SE(표준오차)]

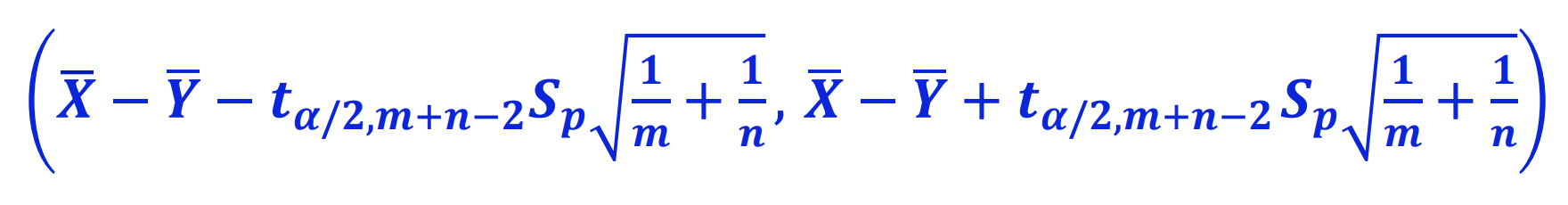
이에 대한 검정 역시 가능한데 H0(귀무가설)은 두 평균의 차이가 같다로 정의하고 귀무가설은 차이가 있다로 정의하여 이를 확인하는 작업을 진행하게 됩니다. 검정통계량은 다음과 같고 델타의 값은 H0에서 같다라고 하였기 때문에 0으로 대체하여 쓸 수 있습니다.
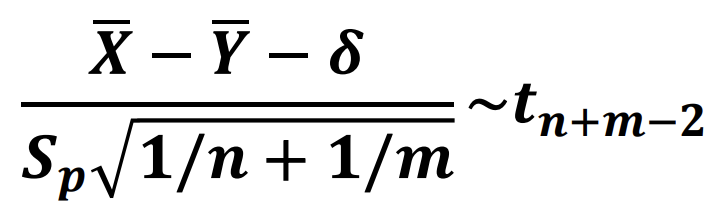
1-2) 분산이 다른 두 집단의 평균 비교
앞서 알아본 과정에서 분산만 다른 두 집단의 평균을 비교하는 과정을 알아보겠습니다. 2개의 집단 X, Y의 표본집단은 다음과 같이 정의할 수 있습니다.

바뀐 조건은 분산이 다를뿐 정규분포를 따르고 두 집단이 독립적이라는 조건에는 변화가 없기 때문에 선형결합 식에서 변화는 각각의 표본분산의 합으로 바뀌었습니다. 또한 이에 따라 표준화를 위한 분모의 식이 달라졌습니다.


앞서 X와 Y의 분산이 같다는 가정으로 합동표본분산을 활용해 중심축량을 구하여 점추정 구간을 구하였습니다. 분산이 경우는 합동이 아니라 각각의 표본분산을 대입할 수 있습니다. 그런데 문제는 그렇게 구한 중심축량이 어떤 분포를 따르는지에 대해서는 아직도 모른다라는 것입니다. 이를 Behrens-Fisher problem(베렌스-피셔 문제)이라고 칭합니다. 그래서 이를 근사한 t-분포로 유도하여 이를 해결하고 있습니다. 이를 위한 자유도가 필요한다 다음과 같은 자유도를 구하여 사용하게 됩니다. 그런데 기존에 사용하던 자유도와 다른 점은 정수가 아닌 실수 형태라는 것입니다. 이 값을 구하기에는 너무 복잡하지만 컴퓨터 프로그램을 사용하면 쉽게 구하기가 가능해졌습니다. 통계와 관련된 모듈에서는 이 값을 계산하여 확인할 수 있습니다. 이후에는 𝝊의 자유도를 따르는 t분포로 앞서 확인한 점 추정 구간을 똑같이 구할 수 있게 됩니다.
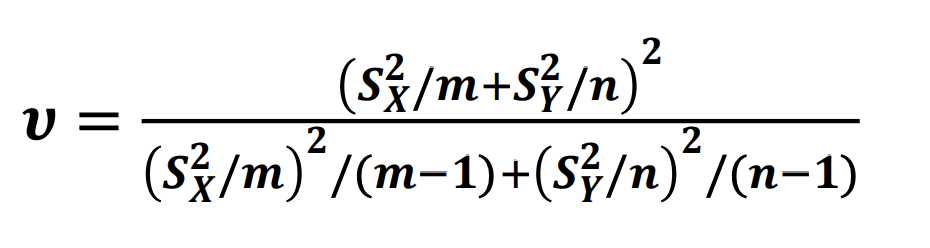
분산이 다른 경우 역시 검정을 진행할 수 있는데 검정통계량은 다음과 같습니다.

이제 Python을 통해서 분산이 같은 경우와 다른 경우에 대한 평균 비교를 진행해보겠습니다. Scipy 모듈에서는 t-test를 지원합니다. t-test란 두 집단의 평균 사이에 유의한 차이가 있는 지 검증하는 가장 보편적인 통계 방법입니다. 위에서 확인한 식들에 직접 대입을 할 필요 없이 표본집단의 평균과 분산에 대한 값을 안다면 쉽게 프로그램을 통해 두 집단의 평균을 비교를 진행할 수 있습니다.
우선 두 그룹의 값을 무작위로 제가 입력했고 이에 대한 BoxPlot을 통해 분포를 확인해보겠습니다.
import numpy as np
groupA = '''
233 291 312 250
246 197 268 224
239 239 254 276
234 181 248 252
202 218 212 325'''.split()
groupB = '''
344 185 263 246
224 212 188 250
148 169 226 175
242 252 153 183
137 202 194 213
'''.split()
groupA = list(map(int,groupA))
groupB = list(map(int,groupB))
## Box plot
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 8))
sns.boxplot(data=[groupA, groupB])
plt.xlabel("Group", fontsize=16)
plt.ylabel("Value", fontsize=16)
plt.xticks([0, 1], ['A','B'], fontsize=14)
plt.show()
이번에는 t-test를 통해서 두 그룹의 평균에 차이가 있는지 없는지 알아보았습니다. 단순히 p-value만 봐보면 양측, 단측 모두 5% 유의수준에서 귀무가설을 기각하므로 평균이 다르다고 할 수 있습니다. 단측 검정의 경우 1% 수준에서도 다르다고 할 수 있는 수준입니다.
(t_test_ind 호출시 'alternative' 옵션으로 양측, 단측 검정을 설정할 수 있고, 'equal_var' 옵션을 통해서 분산이 같은지 다른지를 설정하여 t-test를 진행할 수 있습니다.)
import scipy.stats as stats
# 양측 검정
t_stat, p_val = stats.ttest_ind(groupA, groupB)
print('t-statistic:', t_stat, ' p-value:', p_val)
# 단측 검정
t_stat, p_val = stats.ttest_ind(groupA, groupB, alternative = 'greater') #less
print('t-statistic:', t_stat, ' p-value:', p_val)t-statistic: 2.5621127281853386 p-value: 0.014491988612130562
t-statistic: 2.5621127281853386 p-value: 0.007245994306065281
그런데 주어진 데이터에 대해서 분산이 같은지 정규성을 갖춘것인지에 대한 확인이 필요하겠죠? 이를 확인하는 방법 역시 Python에서 쉽게 구현이 가능하지만 오늘은 두 집단의 평균비교에 포커스를 맞추고 다음 포스팅에서 분산을 확인하는 방법에 대해서 알아보겠습니다.
2) 대응 표본
대응표본의 평균비교는 짝비교라고도 합니다. 그 이유는 하나의 실험 대상에서 나온 두 가지 결과에 대해서 순수한 차이만을 비교하는데 포커스 하는 것입니다. 그래서 아래의 그림의 표와 같이 처리1과 처리2는 i번째 결과는 서로 독립적이지 않습니다. 그래서 앞서 두 집단의 독립적이었을 경우로 비교를 진행할 수 없습니다. 그런데 잘 생각해보면 i, i+1번째의 결과는 서로 독립입니다. 그리고 우리가 알고 싶은것은 처리1과 처리2가 같냐, 차이가 있냐에 중점을 두고 있죠. 그래서 하나의 실험체에서 나온 결과 두가지에 대한 차이를 D라 하면 각각의 D는 독립이 됩니다. 이렇게 되면 우리는 앞서 배운 독립조건을 만족하는 집단의 평균비교로 넘어갈 수 있게 됩니다. 이후 과정은 사실 앞서 알아본 과정과 크게 다를게 없어서 따로 알아보지는 않겠습니다.
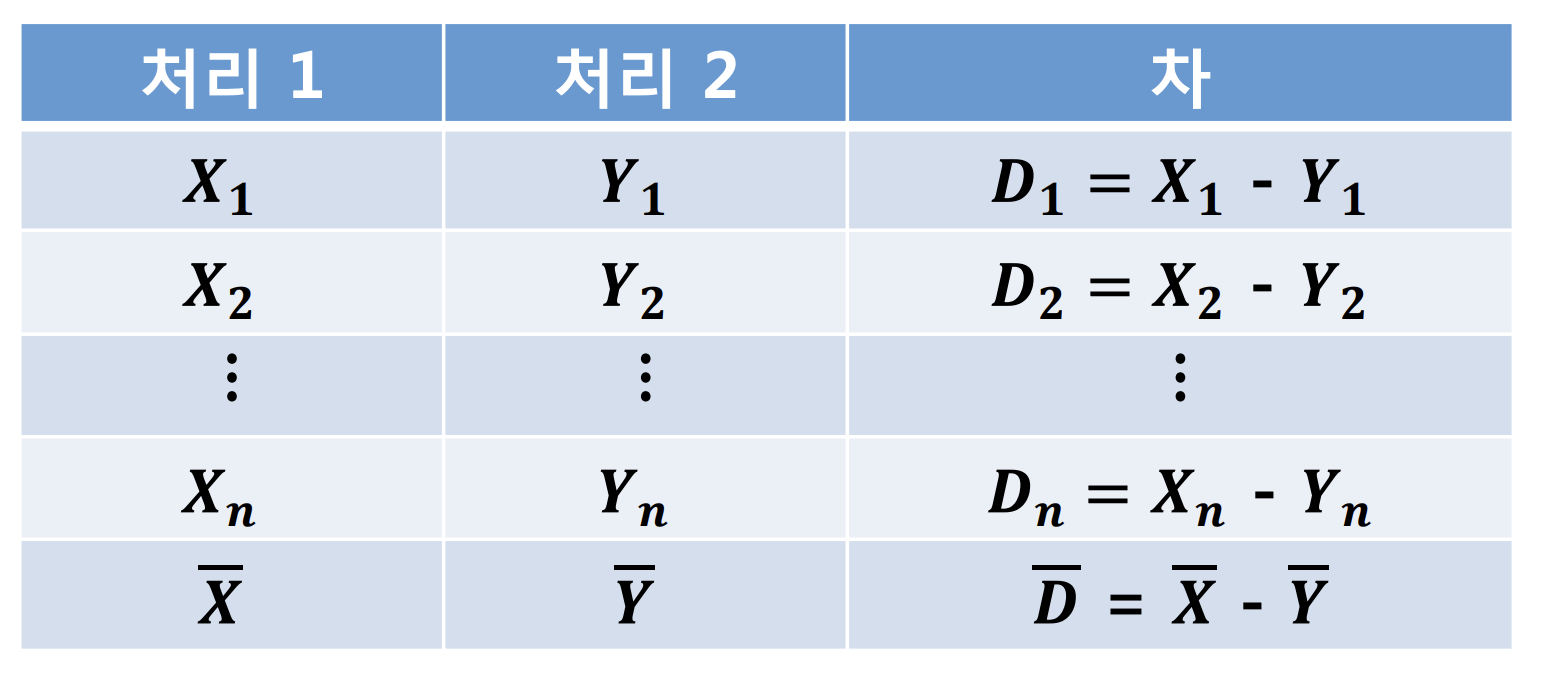
Python을 통해서 대응표본에 대한 평균비교 역시 간단하게 가능합니다. 이번 예시 역시 p-value가 굉장히 낮은 값으로 통계적으로 두 그룹간 평균에 차이가 있다고 할 수 있겠습니다.
X = [117, 108, 105, 89, 101, 93, 96, 108, 108, 94, 93, 112, 92, 91, 100, 96, 120, 86, 96, 95]
Y = [121, 101, 102, 114, 103, 105, 101, 131, 96, 109, 109, 113, 115, 94, 108, 96, 110, 112, 120, 100]
import scipy.stats
scipy.stats.ttest_rel(X, Y)Ttest_relResult(statistic=-2.9868874599588247, pvalue=0.007578486289181322)'통계' 카테고리의 다른 글
| 통계학 - 모평균의 통계적 추론 (0) | 2023.09.27 |
|---|---|
| 통계학 - 추정과 검정(2)_가설과 검정 (0) | 2023.09.26 |
| 통계학 - 추정과 검정(1)_추정법 (0) | 2023.09.25 |
| 기초통계학 - 정규분포(Normal Distribution) (1) | 2023.09.24 |
| 기초 통계학 - 포아송, 기하, 음이항, 다항분포 (1) | 2023.09.22 |




